Verifikation digitaler Systeme

Grundlagen

BDDs

Zerlegung		low child	high child
Shannon	\(f = x \land f_{\lvert x = 1} \lor (\neg x) \land f_{\lvert x = 0}\)	\(f_{\lvert x = 0}\)	\(f_{\lvert x = 1}\)
positive Davio	\(f = f_{\lvert x = 0} \oplus x \land (f_{\lvert x = 1} \oplus f_{\lvert x = 0})\)	\(f_{\lvert x = 0}\)	\(f_{\lvert x = 1} \oplus f_{\vert x = 0}\)
negative Davio	\(f = f_{\lvert x = 1} \oplus (\neg x) \land (f_{\lvert x = 1} \oplus f_{\lvert x = 0})\)	\(f_{\lvert x = 1}\)	\(f_{\lvert x = 1} \oplus f_{\vert x = 0}\)

Simulation und Formale Verifikation

Simulation

Evalulierung des Entwurfs durch Simulation von Stimuli, funktional oder zufällig gewählt.
erfasst nicht das gesamte Verhaltensspektrum
überprüft jeweils genau einen Punkt im Eingaberaum
durch Eingabe getrieben

Formale Verifikation

überprüft Gruppen von Punkten im Eingaberaum
durch Ausgabe getrieben

Steuerbarkeit und Beobachtbarkeit

Steuerbarkeit: wie schwierig ist es, einen bestimmten (internen) Zustand in einem System einzustellen.
Beobachtbarkeit: wie schwierig ist es, einen bestimmten (internen) Zustand eines Systems zu beobachten.

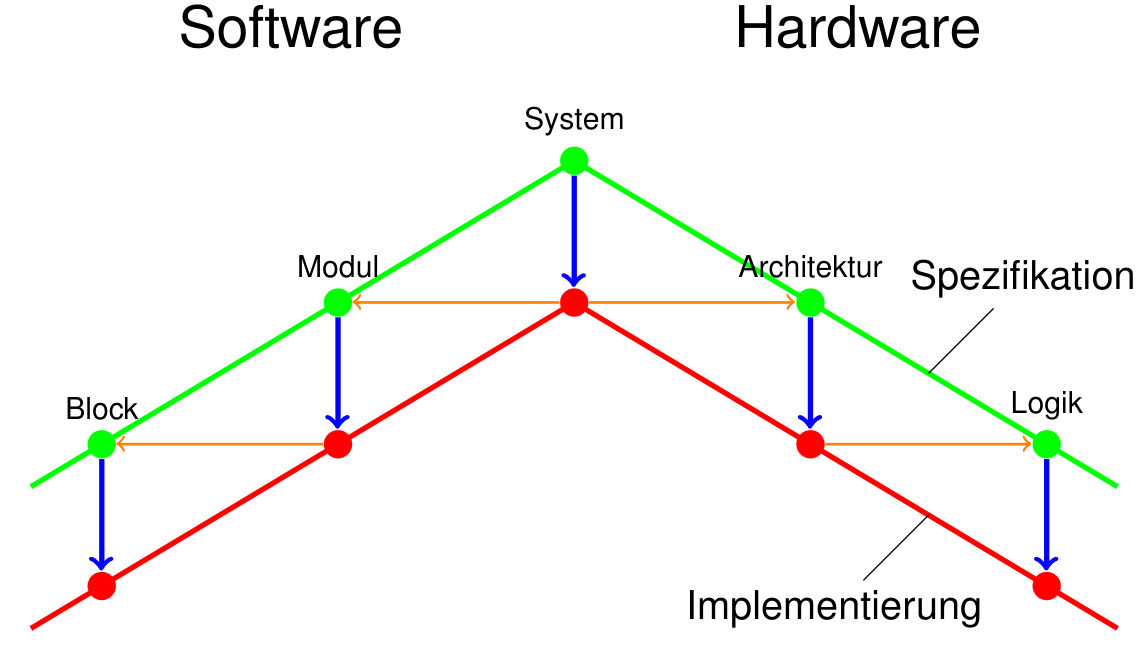
Abstraktion

Strukturelle Abstraktion: Interne Systemdetails werden verborgen
Verhaltensabstraktion: Partielle Spezifikationen, die das Verhalten nicht vollständig beschreiben
Datenabstraktion: Werte auf höheren Abstraktionsebenen darstellen (\(\mathbb{N}\) statt \(\mathbb{B}^n\))
Zeitabstraktion: Zeitraster vergröbern (Befehlszyklen statt Taktzyklen)

Ebene	Verhalten	Struktur	Daten	Zeit
System	Algorithmen	Prozessoren, Busse, Speicher	Zahlen, Unions	Kausalität
Architektur	Mult,Add	ALUs, Multiplizierer	Bitvektoren	Takte
Logik	Boolesche Funktionen	Gatter, FlipFlops	Bits	Gatterlaufzeiten
Modul	Funktionen	Prozesse, OS-Dienste	Zahlen	Takte
Block	Instruktionen	Assemblerbefehle	Bytes	Instruktionsschritte

Äquivalenzprüfung

Automatentheorie

Ein endlicher Zustandsautomat (Mealy) \(M = (S,E,A, \delta, \lambda, s_0)\).

\(S\): endliche Menge von Zuständen
\(E, A\): Ein- und Ausgabealphabet
\(\delta : S \times E \to S\): Überführungsfunktion
\(\lambda : S \times E \to A\): Ausgabefunktion
\(s_0\): Startzustand

Sequenzen

endliche Sequenzen von Eingangssymbolen \(w \in E^+\)
erweiterte Überführungsfunktion \(\delta^+ : S \times E^+ \to S\)
\[ \delta^+ (s,w) := \begin{cases} \delta(s,w) & \lvert w \rvert = 1\\ \delta(\delta^+(s,w_1 \circ \dots \circ w_{\lvert w \rvert - 1}), w_{\lvert w \rvert}) & \lvert w \rvert > 1 \end{cases} \]
erweiterte Ausgabefunktion \(\lambda^+ : S \times E^+ \to S\)
\[ \lambda^+ (s,w) := \begin{cases} \lambda(s,w) & \lvert w \rvert = 1\\ \lambda^+(s,w_1 \circ \dots \circ w_{\lvert w \rvert - 1}) \circ \lambda(\delta^+(s,w_1 \circ \dots \circ w_{\lvert w \rvert - 1}), w_{\lvert w \rvert}) & \lvert w \rvert > 1 \end{cases} \]

Erreichbarkeit

Für \(T \subset S\) sei

\begin{align*} \mathrm{REACH}(T) &:= T \cup \{s \in S \mid \exists t \in T, w \in E^+ .\, \delta^+(t,w) = s\}\\ \mathrm{PRED}(T) &:= \{s \in S \mid \exists t \in T, e \in E .\, \delta(s,e) = t\}\\ \mathrm{SUCC}(T) &:= \{s \in S \mid \exists t \in T, e \in E .\, \delta(t,e) = s\}\\ \end{align*}

Äquivalenzprüfung

Zwei Automaten \(M = (S, E, A, \delta, \lambda, s_0)\) und \(M' = (S', E, A, \delta', \lambda', s_0')\) heißen äquivalent (\(M \equiv M'\)) wenn
\[ \forall w \in E^+ .\, \lambda^+(s_0,w) = \lambda'^+(s'_0, w) \]

Seien \(M = (S, E, A, \delta, \lambda, s_0)\) und \(M = (S', E, A, \delta', \lambda', s_0')\) zwei Automaten und \(s \in S, s' \in S'\) Zustände.
\(s\) und \(s'\) heißen zustandsäquivalent (\(s \sim s'\)), wenn
\[ \forall e \in E .\, \lambda(s,e) = \lambda'(s',e) \land \delta(s,e) \sim \delta'(s',e) \]

Zwei Automaten \(M, M'\) sind genau dann äquivalent, wenn ihre Startzustände äquivalent sind.
\[ ((S, E, A, \delta, \lambda, s_0) \equiv (S', E, A, \delta', \lambda', s_0')) \Leftrightarrow s_0 \sim s'_0 \]

Produktautomaten

Bei der Äquivalenzprüfung müssen nicht alle Kombinationen von Zuständen sondern nur die, in denen die Automaten zum gleichen Zeitpunkt sein können, verglichen werden.

Für zwei Automaten \(M = (S, E, A, \delta, \lambda, s_0)\) und \(M' = (S', E, A, \delta', \lambda', s_0')\) ist der Produktautomat \(M_p\) definiert als

\begin{align*} M_p &:= (S \times S', E, \{0,1\}, \delta_p, \lambda_p, (s_0, s'_0))\\ \delta_p((s,s'), e) &:= (\delta(s,e), \delta'(s',e))\\ \lambda_p((s,s'), e) &:= (\lambda(s,e) =_{\mathbb{B}} \lambda'(s',e)) \end{align*}

und damit für die Zustandsäquivalenz:
\[ s \sim s' \Leftrightarrow \forall e \in E .\, \lambda_p((s,s'), e) = 1 \land \delta_p((s,s'),e) \in \sim \]
und Automatenäquivalenz:
\[ M \equiv M' \Leftrightarrow \forall s \in \mathrm{REACH}(\{(s_0,s'_0)\}), e \in E .\, \lambda_p(s,e) = 1 \]

Äquivalenzprüfung durch Fixpunktiteration

Forward Traversal
1. Starte mit \(S_r \leftarrow \{s_0\}\) und \(S_n \rightarrow S_r\)
2. Wenn \(\exists s \in S_n, e \in E .\, \lambda_p(s,e) = 0\) sind die Automaten nicht äquivalent.
3. Sonst setze \(S_n \leftarrow \delta_p(S_n) \setminus S_r\) und \(S_r \leftarrow S_r \cup S_n\)
  Bis \(S_n = \emptyset\)
Backward Traversal
1. Starte mit \(S_n \leftarrow \{s \in S \mid \exists e \in E .\, \lambda_p(s,e) = 0\}\) und \(S_e \leftarrow S \setminus S_n\)
2. Wenn \(s_0 \in S_n\) dann sind die Automaten nicht äquivalent
3. Sonst setze \(S_n \leftarrow \delta^{-1}(S_n) \cap S_e\) und \(S_e \leftarrow S_e \setminus S_n\)
  Bis \(S_n = \emptyset\)

Repräsentation von Funktionen

Für eine Menge von Funktionen \(F\) heißt \((R,\Phi : R \to F)\) Repräsentation von \(F\) und
\(r \in R\) repräsentiert \(f \in F\), wenn \(\Phi(r) = f\).

Eine Repräsentation \((R, \Phi)\) von \(F\) heißt

vollständig, wenn \(\Phi\) surjektiv ist
eindeutig, wenn \(\Phi\) injektiv ist
kanonisch, wenn \(\Phi\) bijektiv ist

Eine Repräsentation ist sinnvoll wenn sie kanonisch ist, da dann Äquivalenz in der Repräsentation und der Funktionsmenge zusammenfallen.
Außerdem sollten

Operationen wie \(\Phi(r) + \Phi(r')\), \(\Phi(r) \cdot \Phi(r')\) und \(-\Phi(r)\) effizient berechenbar
Substititionen wie \([\Phi(r')/x]\Phi(r)\) effizient durchführbar

sein

Taylorreihen

Für ein Intervall \(I\) und eine beliebig oft differenzierbare Funktion \(f : I \to \mathbb{R}\) ist
\[ P_f(x) := \sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}\cdot(x - a)^n \]
die Taylorreihe mit Entwicklungspunkt \(a \in I\)

TODO Taylorentwicklungsdiagramme (TED)

TODO Symbolisch

Die binäre Kodierung einer Menge \(E\) ist gegeben durch
\[ \sigma_E : E \to \mathbb{B}^n, \text{mit } n \geq \log_2(\lvert E \rvert) \]

Eine boolesche Funktion ist eine Abbildung \(f : \mathbb{B}^n \to \mathbb{B}\).

z.B

\(x_1\)	\(x_2\)	\(x_3\)	\(f(x_1,x_2,x_3)\)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Eine Bewertung ist eine Abbildung \(V \to \mathbb{B}\), wobei \(V\) die Menge der Variablen darstellt.
Eine Boolesche Funktion \(f\) heißt gültig, wenn sie für alle Bewertungen wahr ist
Eine Boolesche Funktion \(f\) heißt erfüllbar, wenn eine wahre Bewertung existiert

Strukturell

Beweise Äquivalenz von System 1 und System 2 durch

Äquivalenzbeweis von Subsystem 1.1 und 2.1
Äquivalenzbeweis von Subsystem 1.2 und 2.2

Probleme stellen dabei False Negatives z.B
Aus System 1 ∼ System 2 und Subssystem 1.1 ∼ 2.1 folgt nicht, dass Subsystem 1.2 ∼ Subsystem 2.2
Da an den Schnittpunkten nicht alle Wertebelegungen einstellbar sein müssen.
Daher:

teurer Erfüllbarkeitstest an den Schnittpunkten
don't-care-Bedingungen
mehrere überlappende Schichten auf Äquivalenz prüfen

OFDDs

Die positive Davio-Dekomposition einer booleschen Funktion \(f\):
\[ f(x_1,\dots,x_n) = f_{\lvert x = 0} \oplus x_i \land (f{\lvert x = 1} \oplus f{\lvert x = 0}) \]

Temporale Aussagenlogik

Eine temporale Struktur \(M = (S,R,L)\) über einer Menge atomarer Formeln \(V\) besteht aus

einer Menge von Zuständen \(S\)
einer linkstotalen Übergangsrelation \(R \subset S \times S\)
einer Markierungsfunktion \(L : S \to \mathcal{P}(V)\)

Ein Pfad in einer temporalen Struktur \(M\) ist eine unendliche Folge \(s = (s_0,s_1,\dots)\) von Zuständen mit
\[ \forall i \in \mathbb{N} .\, (s_i, s_{i + 1}) \in R \]
Der Suffix \(s^{(j)}\) eines Pfades \(s\) ist \(s^{(j)} = (s_j, s_{j+1},\dots)\)

Linear Time Logic (LTL)

Hier gibt es keine Verzweigungen in der temporalen Struktur, d.h. es existiert genau ein Pfad.

Temporaler Operator		Bedeutung
\(\mathrm{X} \Psi\)	next	\(\Psi\) gilt im nächsten Zustand
\(\mathrm{F} \Psi\)	finally	\(\Psi\) gilt in einem Zustand
\(\mathrm{G} \Psi\)	globally	\(\Psi\) gilt in jedem Zustand
\(\Phi \mathrm{U} \Psi\)	until	\(\Phi\) gilt bis zu einem Zustand (der existieren muss) in dem \(\Psi\) gilt
\(\Phi \mathrm{R} \Psi\)	release	\(\Psi\) gilt solange, bis auch \(\Phi\) gilt

Computation Tree Logic (CTL)

Erweitert LTL mit Verzweigungen in der temporalen Struktur und Quantoren:

Pfadquantor	Bedeutung
\(\mathrm{E}\Psi\)	Es existiert ein Pfad in dem \(\Psi\) gilt
\(\mathrm{A}\Psi\)	\(\Psi\) gilt für alle Pfade

Einem LTL-Operator in \(\Psi\) muss immer ein Pfadquantor vorangestellt werden, um eine valide CTL-Formel zu erhalten.
\(\Psi\) muss außerdem quantorenfrei sein (\(\mathrm{AFAG} \Phi\) ist also keine CTL-Formel!).
Somit ergeben sich acht Grundoperatoren mit Basis \(\{\mathrm{EX}, \mathrm{EG}, \mathrm{EU}\}\):

\begin{align*} \mathrm{AX}\Phi &\Leftrightarrow \neg\mathrm{EX}(\neg\Phi)\\ \mathrm{AG}\Phi &\Leftrightarrow \neg\mathrm{EF}(\neg\Phi)\\ \mathrm{AF}\Phi &\Leftrightarrow \neg\mathrm{EG}(\neg\Phi)\\ \mathrm{EF}\Phi &\Leftrightarrow \mathrm{E}(\mathrm{true}\mathrm{U}\Phi)\\ \end{align*}

CTL*

Nicht alle LTL-Formeln lassen sich in CTL ausdrücken, und umgekehrt.

Formel	LTL	CTL	CTL*
\(\mathrm{AFG}\Psi\)	✅	❌	✅
\(\mathrm{EX}\Psi\)	❌	✅	✅
\(\mathrm{AG}\Psi\)	✅	✅	✅
\(\mathrm{EX}\Psi \land \mathrm{AFG}\Psi\)	❌	❌	✅

CTL* übernimmt die temporalen Operatoren von CTL, es muss aber kein Pfadquantor direkt vorangestellt werden und Pfadquantoren dürfen geschachtelt werden.

CTL* ist also ein Superset von CTL und LTL (wobei LTL-Formel implizit \(\mathrm{A}\) -quantifiziert werden).

TODO Formale Eigenschaftsprüfung

Sei \(M = (S,R,L)\) ein endlicher Automat als temporale Struktur mit

\(S\) Menge der Zustände
\(R \subset S \times S\) Übergangsrelation
\(L : S \to \mathcal{P}(V)\) die Label-Funktion

Systemeigenschaften sind {LTL,CTL,CTL*}-Formeln

Identfiziere im Folgenden:

CTL-Formel \(\Phi\) mit der Menge der Zustände \(S_\Phi \subseteq S\) in denen \(\Phi\) gilt
\(\Phi \land \Psi\) mit \(S_\Phi \cap S_Psi\) und \(\Phi \lor \Psi\) mit \(S_\Phi \cup S_\Psi\)
\(\neg\Phi\) mit \(S \setminus S_\Phi\)
\(\mathtt{true}\) mit \(S\) und \(\mathtt{false}\) mit \(\emptyset\)

Sei \(\Phi\) eine Formel und \(y\) eine Variable in \(\Phi\).
Dann ist \(\tau = \lambda y.\, \Phi\) ein Funktional.

Eine Formel \(p\) heißt Fixpunkt eines Funktionals \(\tau\), wenn \(\tau(p) = p\)

Ein Funktional \(\tau\) heißt monoton, wenn \(p \subset q \implies \tau(p) \subset \tau(q)\)

Für ein monotones Funktional \(\tau := \lambda y .\, \Phi\) existiert der kleinste Fixpunkt
\[ \mu y.\, \Phi \]
als Schnitt aller Fixpunkte von \(\tau\)

Für ein monotones Funktional \(\tau := \lambda y .\, \Phi\) existiert der größte Fixpunkt
\[ \nu y.\, \Phi \]
als Vereinigung aller Fixpunkte von \(\tau\)

Sei \(\tau = \lambda y.\, \Phi\) ein monotones Funktional und \(\Phi\) eine CTL-Formel, dann

\begin{align*} \mu y.\, \Phi &= \bigcup_i \tau^i(\mathrm{false})\\ \nu y.\, \Phi &= \bigcap_i \tau^i(true) \end{align*}

Wobei \(\tau^i\) die \(i\) -fache Komposition von \(tau\) mit sich selbst ist (\(\tau^0(p) = p\))

Für CTL-Formel gilt:

\begin{align*} \mathrm{EF}\,p &= \mu y.\, (p \lor \mathrm{EX}\, y)\\ \mathrm{EG}\,p &= \nu y.\, (p \land \mathrm{EX}\, y)\\ \mathrm{E}(p \,\mathrm{U}\,q) &= \mu y.\, (q \lor (p \land \mathrm{EX}\, y))\\ \end{align*}

TODO Symbolic Model Checking

Bounded Model Checking

Grundidee: Restriktiere auf Pfade der Länge \(k\), falte auf und reduziere auf SAT.

Simulationsbasierte Eigenschaftsprüfung

Assertions

statisch: "zero-time"-Bedingungen die funktionale Korrektheit garantieren
temporal: garantieren funktionale Korrektheit über eine Zeitperiode

Überdeckung

Code-Überdeckung

auf einer konkreten Entwurfssprache

Anweisungsüberdeckung: Anteil der durchlaufenden Statements
Grundblocküberdeckung: Anteil der durchlaufenden Blöcke (Statements zu feingranular)
Pfadüberdeckung: Anteil der durchlaufenden Pfade
Zweigüberdeckung: Anteil der durchlaufenden Zweige (nicht äquivalent zu Pfaden!)

Funktionale Überdeckung

auf einem formalen Modell

Parameterüberdeckung

Entwurfssprache oder formales Modell

Softwareverifikation

Uninterpretierte Funktionen

Um von der Funktionalität zu abstrahieren wird nur Kongruenz gefordert:
\[ a = b \implies f(a) = f(b) \]

\begin{align*} \mathtt{msm\, dx, a0, a1} \quad& \mathtt{dx} := f_{\mathrm{add}}(\mathtt{dx}^*, f_{\mathrm{mult}}(\mathtt{a0}^*, \mathtt{a1}^*)\\ \end{align*}

z.B. Äquivalenz zweier C-Programme

a1 = b1 + c1;

tmpB2 = b2;
tmpC2 = c2;
a2 = tmpB2 + tmpC2;

Es ergeben sich schrittweise die Äquivalenzklassen:

\begin{align*} E_1 &:= \{\mathtt{b1},\mathtt{b2},\mathtt{tmpB2}\}\\ E_2 &:= \{\mathtt{c1},\mathtt{c2},\mathtt{tmpC2}\}\\ E_3 &:= \{\mathtt{a1},\mathtt{tmpB2} + \mathtt{tmpC2}\}\\ E_4 &:= \{\mathtt{a2},\mathtt{tmpB2} + \mathtt{tmpC2}\}\\ E_3 &:= \{\mathtt{a1}, \mathtt{a2},\mathtt{tmpB2} + \mathtt{tmpC2}\} \end{align*}

Falschnegative Ergebnisse

Hier entstehen falschnegative Ergebnisse, da z.B. \(f_{\mathrm{mult}}(a,b) = f_{\mathrm{mult}}(b,a)\) nicht herleitbar ist.
Entsprechend werden die nötigen Axiome hinzugefügt.

Falschpositive Ergebnisse

Es wird von konkreten Datentypen abstrahiert (z.B \(\mathbb{R}\) statt Float).
Insbesondere gilt in Float die Identität \((x+y) - z = (x - z) + y\) nicht
Die entsprechenden Datentypen müssen also hinzugefügt werden.

PDG

Symbolische Simulation skaliert schlecht für größere Programme.
Deshalb interessante Stellen (Verifikationsbereiche) mittels PDG wählen.

Ein Program Dependency Graph ist ein bipartiter Graph \((V_P \uplus V_Z, E_C \uplus E_D)\) wobei

\(V_P\) Prädikate von kond. Sprüngen
\(V_Z\) Zuweisungen
\(E_C\) Kontrollfluss
\(E_D\) Datenabhängigkeiten

darstellen

Statische Analyse

Konkrete Interpretation: führe Programm aus und teste Wertebereich
Abstrakte Interpretation: teste Wertebereiche
Vorzeichen-Wertebereich: pos,neg,zero
Kongruenz-Wertebereich: \(x \bmod k\) für \(k \in \mathbb{N}\)
Intervall-Wertebereich: \(\{[a,b] \mid a \leq b, a,b \in \mathbb{Z}\}\)

Hoare-Logik

siehe SemProg

Zeitanalyse

Core Execution Time: Ausführungszeit ohne Unterbrechungen
Best Case Execution Time (BCET): Bestmögliche Ausführungszeit
Worst Case Execution Time (WCET): Schlechtestmögliche Ausführungszeit

Die Analyse kann in zwei (nicht unabhängige) Teilprobleme zerlegt werden:

Programmpfadanalyse

welche Ausführungspfade führen zur schnellsten/langsamsten Ausführung

Modellierung der Zielarchitektur

Architekturmerkmale wie Caches, Pipelining usw.
Hierbei gibt es die Möglichkeiten:

Instruction Time Addition: Annahme: jede Instruktion hat konstante Ausführungszeit
Path Segment Simulation: zyklenakurate Modellierung

Echtzeitscheduling

Ein Task-Graph ist ein Tupel \(G = (V,E)\) mit

\(V\) Menge der Tasks
\(E \subset V \times V\) Menge der Task-abhängigkeiten
\(t_d : V \to \mathbb{R} \cup \{\infty\}\) ordnet jedem Task eine Deadline zu
\(\Delta t : V \to \mathbb{R}\) ordnet jedem Task eine Ausführungsdauer zu

Für einen Ablaufplan

\(t_s,t_e : V \to \mathbb{R}\) ordnen jedem Task Start- und Endzeitpunkt zu
\(t_L(v) := t_e(v) - t_d(v)\) ordnet jedem Task seine Lateness (d.h Abweichung des Endzeitpunkts von der Deadline) zu

Earliest-due-date (EDD)

Sortiere Task aufsteigend nach Deadlines.
Erzeugt einen Ablaufplan mit minimaler maximaler Lateness
\[ \underset{\text{Ablaufpläne}}{\mathrm{argmin}}\left\{ \max_{v \in V}t_L(v)\right\} \]

Latest-deadline-first (LDF)

iterativ Task einreihen der
- keine uneingereihten nachfolgenden Tasks hat
- die größte Deadline hat
drehe die Ergebnisliste um

Erzeugt einen Ablaufplan mit minimaler maximaler Lateness

Earliest-deadline-first (EDF)

Weitere Bedingungen:

\(t_r : V \to \mathbb{R}\) ordnet jedem Task den Zeitpunkt zu, ab dem er gestartet werden kann (Release-Zeit)

EDD erzeugt damit Ablaufpläne mit unnötig hoher maximaler Lateness.

Deshalb:

Nehme an, dass Tasks unterbrochen werden können
Taskwechsel kosten keine Zeit
Springe zum nächsten signifikanten Zeitpunkt (Task fertig oder Task erreicht Release-Zeit)
Wähle Task \(v^*\) mit kürzester Deadline
Unterscheide:
- der aktuelle Task ist \(v^*\) → v^* läuft weiter
- sonst → unterbreche den aktuellen Task und starte \(v^*\)
goto 1.

TODO Systemverifikation

Systeme können vor der Einteilung in Hardware/Software beschrieben werden.

SystemC

Module realisieren eine konkrete Entität
Ports erlauben die Kommunikation aus einem Modul heraus
Signale und Channels modellieren die Kommunikationskanäle
Methoden führen Operationen aus, getriggert durch Sensitivitätsliste
Threads führen Operationen aus, starten automatisch

1-Bit Multiplizierer

SC_MODULE(one_bit_multi){
  sc_in<bool> a,b;
  sc_out<bool> f;

  void compute() {
    f = a && b;
  }

  SC_CTOR(one_bit_multi) {
    SC_METHOD(compute);
    sensitive << a << b;
  }
};

SC_MODULE(stim_gen){
  sc_out<bool> a,b;

  void send_values() {

    a = true;
    b = true;
    wait(5, SC_NS);

    a = false;
    b = true;
    wait(5, SC_NS);

    a = false;
    b = false;
    wait(5, SC_NS);
  }

  SC_CTOR(stim_gen) {
    SC_THREAD(send_values);
  }
};

int sc_main(int, char* []) {
  sc_signal<bool> a, b, f;
  one_bit_multi mul("Multiplizierer");
  stim_gen generator("Tester");

  mul.a(a);
  mul.b(b);
  mul.f(f);

  generator.a(a);
  generator.b(b);

  sc_start();
  return 0;
}

TODO Transaction Level Model

Transaktionen sind die Abstraktion der Kommunikation zwischen nebenläufigen Prozessen.
In SystemC sind Transaktionen

blockierend
nicht-blockierend

und

loosely timed
approximately timed
cycle accurate